斐波那契数列的定义如下:
\[
f_n = \begin{cases}
1, & n = 1, 2\\
f_{n-1} + f_{n-2}, &n > 2
\end{cases}
\]
根据这个我们不难写出 递归 方式求解斐波那契数列的代码:
\[
\begin{array}{l}
\text{Fibonacci-Recursive}(n)\\
\begin{array}{ll}
1 & \textbf{if } n < 2 \\
2 & \qquad\textbf{return } 1 \\
3 & \textbf{else} \\
4 & \qquad\textbf{return } \text{Fibonacci-Recursive}(n-1) + \text{Fibonacci-Recursive}(n-2)
\end{array}
\end{array}
\]
然而通过简单的实验,可以发现这种方式效率极低:

其时间复杂度 \(T(n) = T(n-1) + T(n-2)\),可以推导出为 \(O(2^n)\) 的。造成如此的效率低下的原因就是 进行了太多次重复的运算。如果我们将递归求解的过程化成一棵树,我们可以发现其中有太多太多重复的部分:
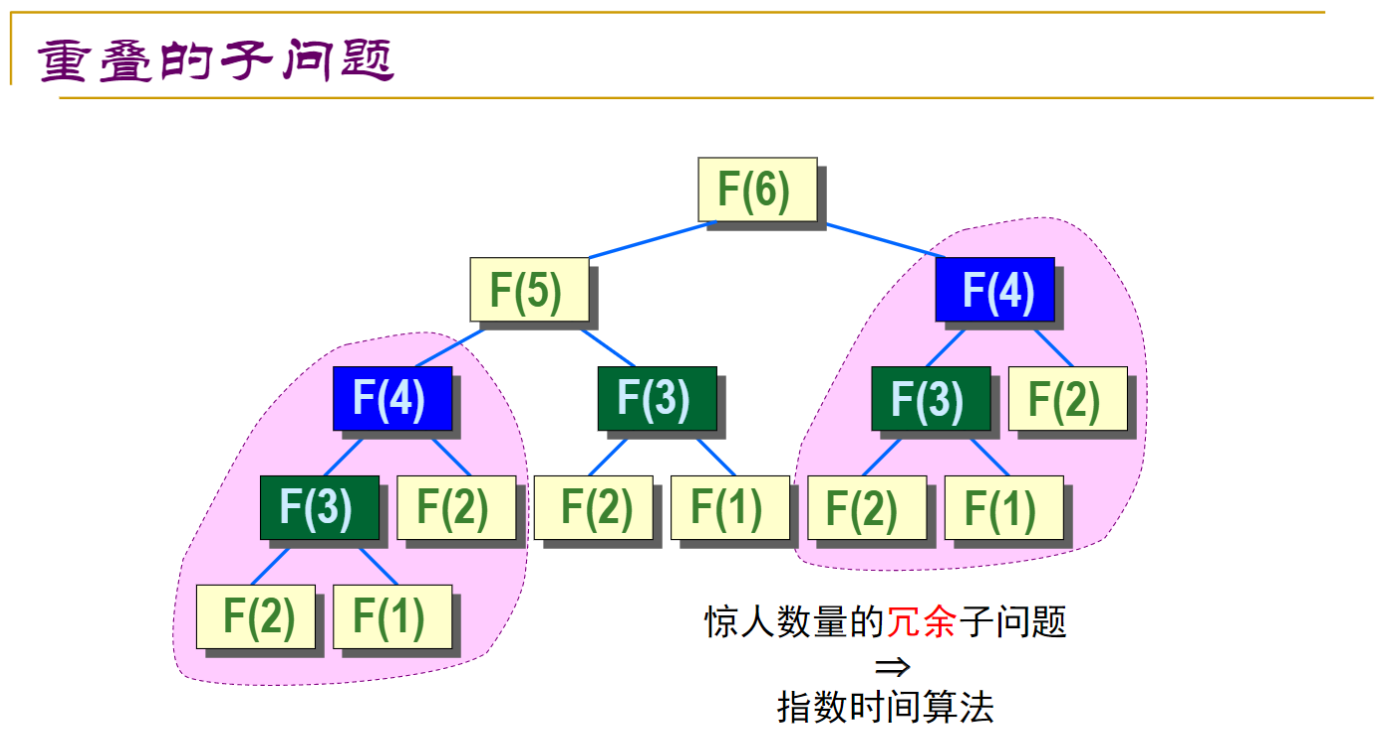
另一种方法是以递推的方式进行求解:
\[
\begin{array}{l}
\text{Fibonacci-Iteration}(n)\\
\begin{array}{ll}
1 & F_1 \leftarrow 1, F_2 \leftarrow 1\\
2 & \textbf{for } i \leftarrow 3 \textbf{ to } n \\
3 & \qquad F_i \leftarrow F_{i-1} + F_{i-2}\\
4 & \textbf{return } F_n
\end{array}
\end{array}
\]
如此其时间复杂度是线性的,能够解决上述递归方式重复计算子问题导致效率低下的问题。
另外还有一种方式,通过对递归方式加一点修改也可以解决这个问题。那就是 记忆化搜索,将搜索过程中的结果保存下来,并在之后的搜索过程中加以利用:
\[
\begin{array}{l}
\text{Fibonacci-Recursive-Memorized}(n)\\
\begin{array}{ll}
1 & \textbf{if } F_i = NIL\\
2 & \qquad\textbf{if } n < 2 \\
3 & \qquad\qquad F_i \leftarrow 1 \\
4 & \qquad\textbf{else} \\
5 & \qquad\qquad F_i \leftarrow \text{Fibonacci}(n-1) + \text{Fibonacci}(n-2) \\
6 & \textbf{return } F_i
\end{array}
\end{array}
\]
目标:给定面值分别为1元、5元、10元的硬币(每种都有足够多枚),请设计一个算法,可以使用最少数量的硬币向客
户支付给定金额。
如果还有面值为7元的硬币,那么贪婪算法可能就无法得到最优解了
- 例如凑出19元,贪婪算法需要使用4枚硬币(10+7+1+1),但事实上只需要3枚硬币(7+7+5)
对于给定的硬币组,如何找到凑成给定金额 n 的最小硬币数?
每一次选择必定要从 1、5、7、10 中选一个,于是可以据此将选择分为四种情形:
- 给一枚面值为 1 元的硬币,此时仍需给顾客 n-1 元
- 给一枚面值为 5 元的硬币,此时仍需给顾客 n-5 元
- 给一枚面值为 7 元的硬币,此时仍需给顾客 n-7 元
- 给一枚面值为 10 元的硬币,此时仍需给顾客 n-10 元
而为了保证最终的金额最小,上面的 n-1、n-5、n-7、n-10 要以最优方式拼凑出来。
分别计算以上情形后选择一个最佳方案即可。
\[
\begin{array}{l}
\text{Find-Recursive}(n)\\
\begin{array}{ll}
1 & \textbf{if } n = 0 \textbf{ then return } 0\\
2 & \textbf{if } n < 0 \textbf{ then return } \infty\\
3 & \textbf{return } \min\{\\
& \qquad \text{Find-Recursive}(n-1) + 1,\\
& \qquad \text{Find-Recursive}(n-5) + 1,\\
& \qquad \text{Find-Recursive}(n-7) + 1,\\
& \qquad \text{Find-Recursive}(n-10) + 1\\
& \}
\end{array}
\end{array}
\]
但是。。这不就是暴力搜索么。
假如将问题一般化,对于目标数值 \(n\) 和 \(m\) 种面值分别为 \(d_1, d_2, \cdots, d_m\) 的硬币,当 \(n\) 和 \(m\) 更时,这种算法的效率将极其低下,原因依旧是太多的 重复计算。
我们能不能依旧按照 一 中的思路,使用递推来降低时间复杂度呢?
可以发现,我们要想求解 \(n\) 元的问题,就要先求解 \(n-d_1, n-d_2, \cdots, n-d_m\) 元的问题,以此类推直到求解 \(d_1\) 元的问题,此时只有一个选项,就是选它。
那么我们可以换一种思路,从 \(d_1\) 元的问题开始,利用已知的信息逐步推演得到 \(d_1 + d_1, d_1 + d_2, \cdots d_1 + d_m\) 元的问题的答案,以此类推利用已知的信息推演出所有最优情况,最终确定 \(n\) 元的问题的答案:
\[
\begin{array}{l}
\text{Find-Iteration}(n)\\
\begin{array}{ll}
1 & F_0 \leftarrow 0\\
2 & \textbf{for } i \leftarrow 1 \textbf{ to } n\\
3 & \qquad\textbf{for } j \leftarrow 1 \textbf{ to } m\\
4 & \qquad\qquad\textbf{if } i - d_j > 0\\
5 & \qquad\qquad\qquad F_i \leftarrow \min(F_i, F_{i-d_j} + 1)\\
6 & \textbf{return } F_n
\end{array}
\end{array}
\]
咕
首先先回顾一下矩阵的乘法:
\[
\begin{pmatrix}
\colorbox{#aaffff}{$a_{11}$} & \colorbox{#aaffff}{$a_{12}$}\\
a_{21} & a_{22}\\
a_{31} & a_{32}\\
\end{pmatrix}
\times
\begin{pmatrix}
\colorbox{#aaffff}{$b_{11}$} & b_{12} & b_{13}\\
\colorbox{#aaffff}{$b_{21}$} & b_{22} & b_{23}\\
\end{pmatrix} = \begin{pmatrix}
\colorbox{#aaffff}{$a_{11}b_{11} + a_{12}b_{21}$} & a_{11}b_{12} + a_{12}b_{22} & a_{11}b_{13} + a_{12}b_{23}\\
a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22} & a_{21}b_{13} + a_{22}b_{23}\\
a_{31}b_{11} + a_{32}b_{21} & a_{31}b_{12} + a_{32}b_{22} & a_{31}b_{13} + a_{32}b_{23}\\
\end{pmatrix}
\]
可以写作:
\[
c_{i,j} = \sum_{k = 1}^q a_{i,k}b_{k,j}
\]
很容易可以写出其伪代码:
\[
\begin{array}{l}
\text{Matrix-Multiply}(A_{p \times q}, B_{q \times r})\\
\textbf{Notes. }A, B, C \text{ are matrix, and } a_{i,j}, b_{i, j}, c_{i, j} \text{ are the elements in the matrix}\\
\begin{array}{ll}
1 & \textbf{for } i \leftarrow 1 \textbf{ to } p\\
2 & \qquad\textbf{for } j \leftarrow 1 \textbf{ to } r\\
3 & \qquad\qquad c_{i, j} \leftarrow 0\\
4 & \qquad\qquad\textbf{for } k \leftarrow 1 \textbf{ to } q\\
5 & \qquad\qquad\qquad c_{i, j} \leftarrow c_{i,j} + a_{i, k} \times b_{k, j}\\
6 & \textbf{return } C_{p \times r}
\end{array}
\end{array}
\]
当对多个矩阵进行链式乘积时,以何种顺序进行运算就成为了一个影响性能的至关重要的问题。
例如我们有这样三个矩阵:\(A_{10 \times 100}, B_{100 \times 5}, C_{5 \times 50}\)
两种截然不同的方式将导致完全不同的元素乘法次数:
\((AB)C = D_{10 \times 5} \cdot C_{5 \times 50}\):共 \(10 \cdot 100 \cdot 5 + 10 \cdot 5 \cdot 50 = 7,500\) 次元素乘法
\(A(BC) = A_{10 \times 100} \cdot E_{100 \times 50}\):共 \(10 \cdot 100 \cdot 50 + 100 \cdot 5 \cdot 50 = 75,000\) 次元素乘法
矩阵链乘积问题如下:
对于给定矩阵序列 \(A_1, A_2, \cdots, A_n\),其中 \(A_i\) 的阶数为 \(P_{i-1} \times P_{i}\),试确定矩阵相乘的次序使得元素乘法总次数最少。
每一次乘法相当于将整个矩阵序列划分为两部分,将相邻处的两个矩阵“合并”:
$$
A_{i..j} = A_{i..k} \times A_{k+1..j}
$$
若令 \(F_{i,j}\) 表示 \(A_{i..j}\) 中元素乘法的次数,那么可以知道对于任意的 \(k\) 有:
$$
F_{i,j} = F_{i,k} + P_{i-1} \cdot P_{k} \cdot P_{j} + F_{k+1,j}
$$
那么对于某一个 \(i, j\),只要得出对于任意的 \(i \leq k < j\) 的元素乘法次数,再求最小值即可。同时也要使 $F_{i, k} $ 和 \(F_{k+1, j}\) 最小。
现在我们直接列出其递推式:
\[
F_{i, j} = \begin{cases}
0, &i = j\\
\min_{i \leq k < j} \{ F_{i, k} + P_{i-1}P_kP_j + F_{k+1, j}\}, & i < j
\end{cases}
\]
伪代码如下:
\[
\begin{array}{l}
\text{Matrix-Chain-Order}\\
\textbf{Input. } P_0, P_1, \cdots, P_n\\
\textbf{Output. } \text{ cost table } M \text{ and divide table } S\\
\textbf{Notes. } \text{m, s are the elements of M and S}\\
\begin{array}{ll}
1 & \textbf{for } i \leftarrow 1 \textbf{ to } n\\
2 & \qquad m_{i, i} \leftarrow 0, s_{i, i} \leftarrow 0\\
3 & \textbf{for } l \leftarrow 2 \textbf{ to } n\\
4 & \qquad\textbf{for } i \leftarrow 1 \textbf{ to } n - l + 1\\
5 & \qquad\qquad j \leftarrow i + l - 1\\
6 & \qquad\qquad m_{i, j} \leftarrow \infty\\
7 & \qquad\qquad\textbf{for } k \leftarrow i \textbf{ to } j-1\\
8 & \qquad\qquad\qquad q \leftarrow m_{i, k} + P_{i-1} \times P_k \times P_j + m_{k+1, j}\\
9 & \qquad\qquad\qquad \textbf{if } q < m_{i, j}\\
10 & \qquad\qquad\qquad\qquad m_{i, j} \leftarrow q\\
11 & \qquad\qquad\qquad\qquad s_{i, j} \leftarrow k\\
12 & \textbf{return } M, S
\end{array}
\end{array}
\]

